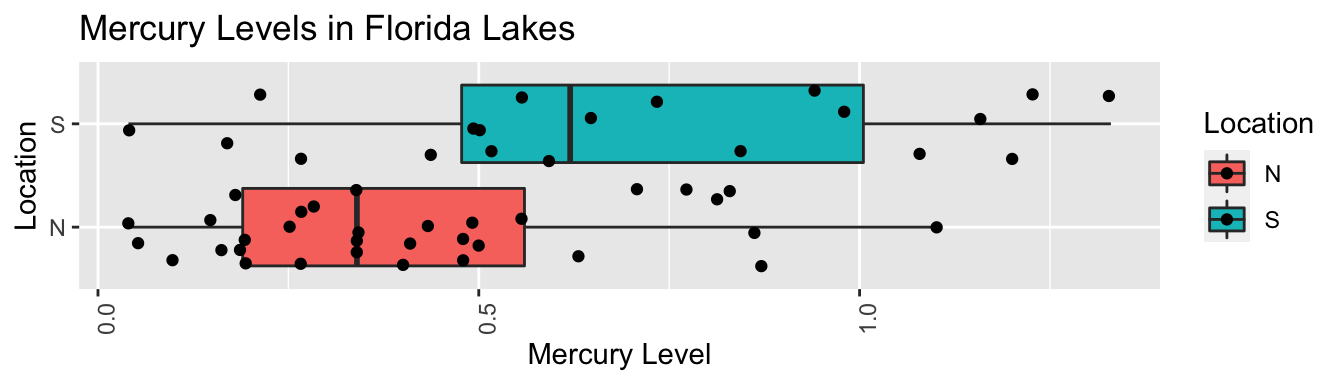
ggplot(data=FloridaLakes, aes(x=Location, y=AvgMercury, fill=Location)) + geom_boxplot() + geom_jitter() + ggtitle("Mercury Levels in Florida Lakes") + xlab("Location") + ylab("Mercury Level") + theme(axis.text.x = element_text(angle = 90)) + coord_flip()
FloridaLakes %>% group_by(Location) %>% summarize(MeanHg=mean(AvgMercury), StDevHg=sd(AvgMercury), N=n())## # A tibble: 2 x 4 ## Location MeanHg StDevHg N ## ## 1 N 0.425 0.270 33 ## 2 S 0.696 0.384 20 Lakes_M lm(data=FloridaLakes, AvgMercury ~ Location) summary(Lakes_M)## ## Call: ## lm(formula = AvgMercury ~ Location, data = FloridaLakes) ## ## Residuals: ## Min 1Q Median 3Q Max ## -0.65650 -0.23455 -0.08455 0.24350 0.67545 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 0.42455 0.05519 7.692 0.000000000441 *** ## LocationS 0.27195 0.08985 3.027 0.00387 ** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.3171 on 51 degrees of freedom ## Multiple R-squared: 0.1523, Adjusted R-squared: 0.1357 ## F-statistic: 9.162 on 1 and 51 DF, p-value: 0.003868Key Question:
We can answer the key question using simulation.
We’ll simulate situations where there is no relationship between location and mercury level, and see how often we observe a value of \(b_1\) as extreme as 0.27195.
Procedure:
ShuffledLakes FloridaLakes ## create copy of dataset ShuffledLakes$Location ShuffledLakes$Location[sample(1:nrow(ShuffledLakes))] | Lake | Location | AvgMercury | Shuffled Location |
|---|---|---|---|
| Alligator | S | 1.23 | N |
| Annie | S | 1.33 | N |
| Apopka | N | 0.04 | N |
| Blue Cypress | S | 0.44 | N |
| Brick | S | 1.20 | N |
| Bryant | N | 0.27 | S |
Recall this model was fit under an assumption of no relationship between location and average mercury.
M_Lakes_Shuffle lm(data=ShuffledLakes, AvgMercury~Location) summary(M_Lakes_Shuffle)## ## Call: ## lm(formula = AvgMercury ~ Location, data = ShuffledLakes) ## ## Residuals: ## Min 1Q Median 3Q Max ## -0.4891 -0.2591 -0.0440 0.2460 0.8009 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 0.529091 0.059944 8.826 0.00000000000761 *** ## LocationS -0.005091 0.097582 -0.052 0.959 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.3444 on 51 degrees of freedom ## Multiple R-squared: 5.336e-05, Adjusted R-squared: -0.01955 ## F-statistic: 0.002722 on 1 and 51 DF, p-value: 0.9586 ShuffledLakes FloridaLakes ## create copy of dataset ShuffledLakes$Location ShuffledLakes$Location[sample(1:nrow(ShuffledLakes))] kable(head(Shuffle1df))| Lake | Location | AvgMercury | Shuffled Location |
|---|---|---|---|
| Alligator | S | 1.23 | N |
| Annie | S | 1.33 | N |
| Apopka | N | 0.04 | N |
| Blue Cypress | S | 0.44 | N |
| Brick | S | 1.20 | N |
| Bryant | N | 0.27 | S |
Recall this model was fit under an assumption of no relationship between location and average mercury.
M_Lakes_Shuffle lm(data=ShuffledLakes, AvgMercury~Location) summary(M_Lakes_Shuffle)## ## Call: ## lm(formula = AvgMercury ~ Location, data = ShuffledLakes) ## ## Residuals: ## Min 1Q Median 3Q Max ## -0.51485 -0.27485 -0.05485 0.27515 0.77515 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 0.55485 0.05961 9.308 0.00000000000141 *** ## LocationS -0.07335 0.09704 -0.756 0.453 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.3425 on 51 degrees of freedom ## Multiple R-squared: 0.01108, Adjusted R-squared: -0.008313 ## F-statistic: 0.5713 on 1 and 51 DF, p-value: 0.4532 ShuffledLakes FloridaLakes ## create copy of dataset ShuffledLakes$Location ShuffledLakes$Location[sample(1:nrow(ShuffledLakes))] kable(head(Shuffle1df))| Lake | Location | AvgMercury | Shuffled Location |
|---|---|---|---|
| Alligator | S | 1.23 | N |
| Annie | S | 1.33 | N |
| Apopka | N | 0.04 | N |
| Blue Cypress | S | 0.44 | N |
| Brick | S | 1.20 | N |
| Bryant | N | 0.27 | N |
Recall this model was fit under an assumption of no relationship between location and average mercury.
M_Lakes_Shuffle lm(data=ShuffledLakes, AvgMercury~Location) summary(M_Lakes_Shuffle)## ## Call: ## lm(formula = AvgMercury ~ Location, data = ShuffledLakes) ## ## Residuals: ## Min 1Q Median 3Q Max ## -0.56200 -0.26200 -0.08182 0.22818 0.74818 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 0.48182 0.05905 8.16 0.0000000000818 *** ## LocationS 0.12018 0.09612 1.25 0.217 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.3392 on 51 degrees of freedom ## Multiple R-squared: 0.02974, Adjusted R-squared: 0.01072 ## F-statistic: 1.563 on 1 and 51 DF, p-value: 0.2169 ShuffledLakes FloridaLakes ## create copy of dataset ShuffledLakes$Location ShuffledLakes$Location[sample(1:nrow(ShuffledLakes))] kable(head(Shuffle1df))| Lake | Location | AvgMercury | Shuffled Location |
|---|---|---|---|
| Alligator | S | 1.23 | N |
| Annie | S | 1.33 | S |
| Apopka | N | 0.04 | S |
| Blue Cypress | S | 0.44 | N |
| Brick | S | 1.20 | N |
| Bryant | N | 0.27 | N |
Recall this model was fit under an assumption of no relationship between location and average mercury.
M_Lakes_Shuffle lm(data=ShuffledLakes, AvgMercury~Location) summary(M_Lakes_Shuffle)## ## Call: ## lm(formula = AvgMercury ~ Location, data = ShuffledLakes) ## ## Residuals: ## Min 1Q Median 3Q Max ## -0.5261 -0.2730 -0.0630 0.2470 0.7639 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 0.56606 0.05929 9.548 0.00000000000061 *** ## LocationS -0.10306 0.09651 -1.068 0.291 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.3406 on 51 degrees of freedom ## Multiple R-squared: 0.02187, Adjusted R-squared: 0.002691 ## F-statistic: 1.14 on 1 and 51 DF, p-value: 0.2906 ShuffledLakes FloridaLakes ## create copy of dataset ShuffledLakes$Location ShuffledLakes$Location[sample(1:nrow(ShuffledLakes))] kable(head(Shuffle1df))| Lake | Location | AvgMercury | Shuffled Location |
|---|---|---|---|
| Alligator | S | 1.23 | N |
| Annie | S | 1.33 | N |
| Apopka | N | 0.04 | N |
| Blue Cypress | S | 0.44 | S |
| Brick | S | 1.20 | S |
| Bryant | N | 0.27 | N |
Recall this model was fit under an assumption of no relationship between location and average mercury.
M_Lakes_Shuffle lm(data=ShuffledLakes, AvgMercury~Location) summary(M_Lakes_Shuffle)## ## Call: ## lm(formula = AvgMercury ~ Location, data = ShuffledLakes) ## ## Residuals: ## Min 1Q Median 3Q Max ## -0.50455 -0.24850 -0.05455 0.22545 0.78545 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 0.54455 0.05981 9.104 0.00000000000286 *** ## LocationS -0.04605 0.09737 -0.473 0.638 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.3436 on 51 degrees of freedom ## Multiple R-squared: 0.004366, Adjusted R-squared: -0.01516 ## F-statistic: 0.2236 on 1 and 51 DF, p-value: 0.6383 b1 Lakes_M$coef[2] ## record value of b1 from actual data ## perform simulation b1Sim rep(NA, 10000) ## vector to hold results ShuffledLakes FloridaLakes ## create copy of dataset for (i in 1:10000) #randomly shuffle locations ShuffledLakes$Location ShuffledLakes$Location[sample(1:nrow(ShuffledLakes))] ShuffledLakes_M lm(data=ShuffledLakes, AvgMercury ~ Location) #fit model to shuffled data b1Sim[i] ShuffledLakes_M$coef[2] ## record b1 from shuffled model > NSLakes_SimulationResults data.frame(b1Sim) #save results in dataframe NSLakes_SimulationResultsPlot ggplot(data=NSLakes_SimulationResults, aes(x=b1Sim)) + geom_histogram(fill="lightblue", color="white") + geom_vline(xintercept=c(b1, -1*b1), color="red") + xlab("Lakes: Simulated Value of b1") + ylab("Frequency") + ggtitle("Distribution of b1 under assumption of no relationship") NSLakes_SimulationResultsPlot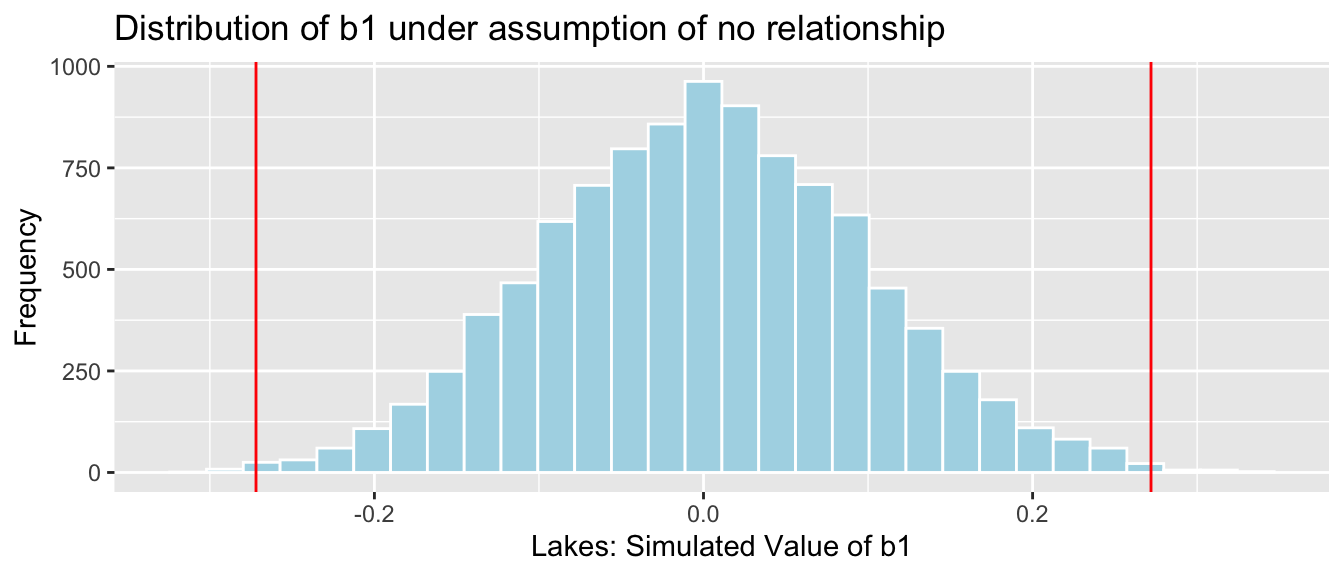
It appears unlikely that we would observe a value of \(b_1\) as extreme as 0.27195 ppm by chance, if there is really no relationship between location and mercury level.
Number of simulations resulting in simulation value of \(b_1\) more extreme than 0.27195.
sum(abs(b1Sim) > abs(b1))## [1] 31Proportion of simulations resulting in simulation value of \(b_1\) more extreme than 0.27195.
mean(abs(b1Sim) > abs(b1))## [1] 0.0031The probability of observing a value of \(b_1\) as extreme as 0.27195 by chance, when there is no relationship between location and mercury level is very low.
There is strong evidence of a relationship between location and mercury level. In this case, there is strong evidence that mercury level is higher in Southern Lakes than northern Lakes.
## 2.5% 97.5% ## 0.08095682 0.46122992 NS_Lakes_Bootstrap_Plot_b1 + geom_vline(xintercept = c(q.025, q.975), color="red")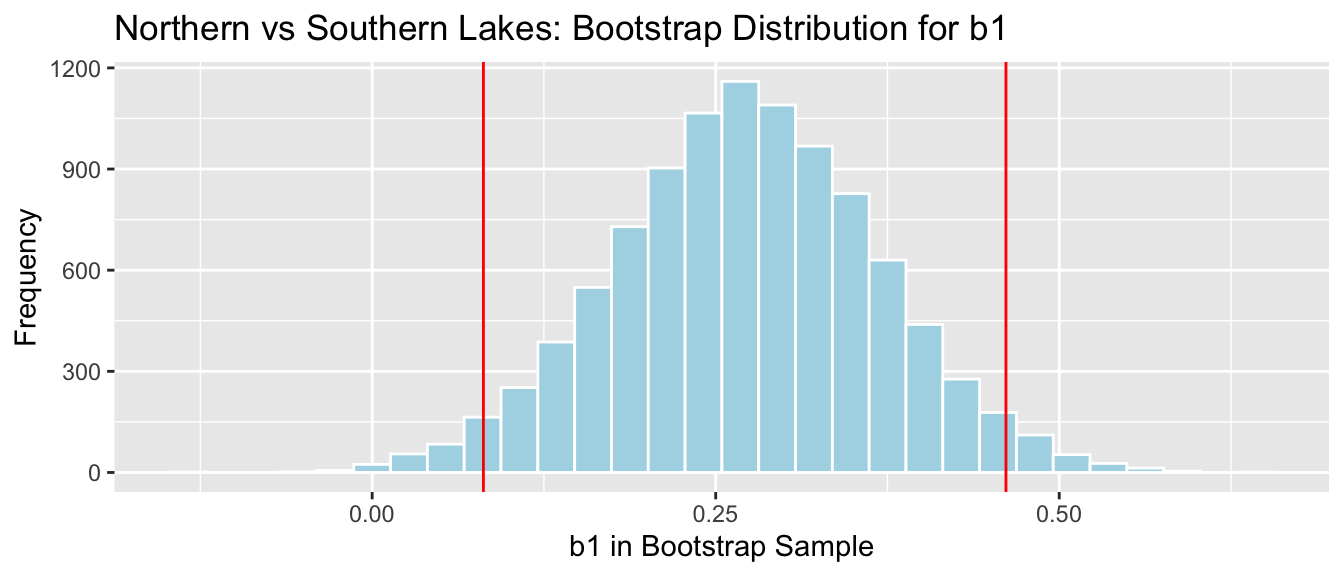
We are 95% confident the average mercury level in Southern Lakes is between 0.08 and 0.46 ppm higher than in Northern Florida.
The fact that the interval does not contain 0 is consistent with the hypothesis test.
We can think of the simulation as a test of the following hypotheses:
Hypothesis 1: There is no relationship between location and mercury level. (Thus the difference of 0.27 we observed in our data occurred just by chance).
Hypothesis 2: The difference we observed did not occur by chance (suggesting a relationship between location and mercury level).
The “no relationship,” or “chance alone” hypothesis is called the null hypothesis. The other hypothesis is called the alternative hypothesis.
We used \(b_1\) to measure difference in mean mercury levels between the locations in our observed data.
We found that the probability of observing a difference as extreme as 0.27 when Hypothesis 1 is true is very low (approximately 0.0017)
knitr::include_graphics("pvals.png")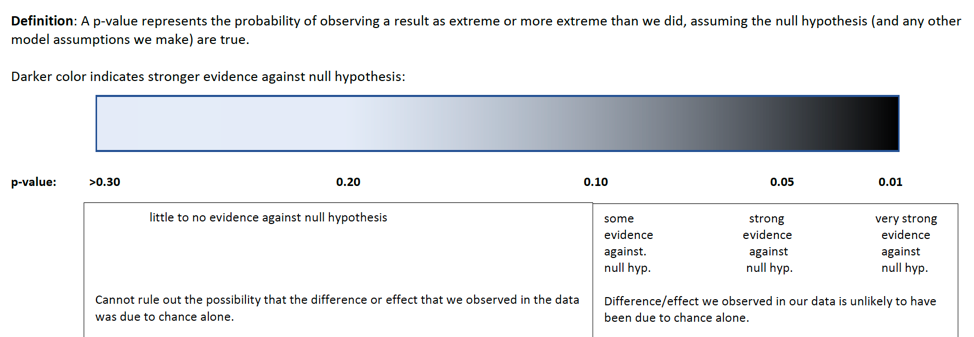
ggplot(data=Cars2015, aes(x=Acc060, y=LowPrice)) + geom_point() + stat_smooth(method="lm", se=FALSE)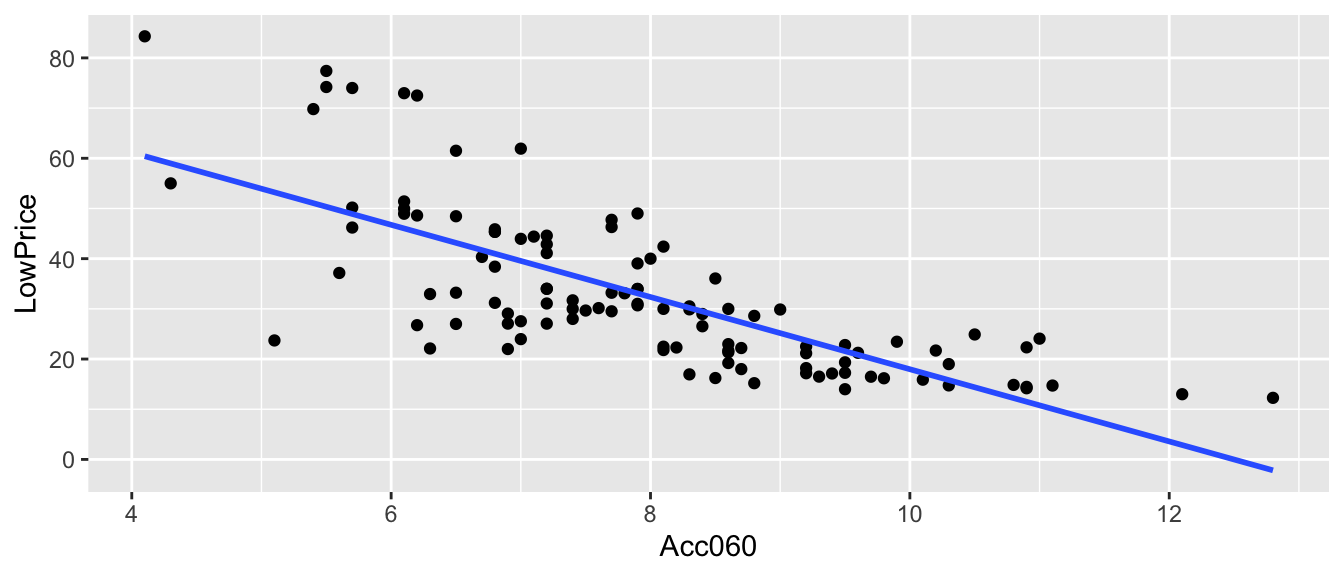
\(\widehat = b_0+b_1\times \text =89.9036 -7.1933\times\text\)
Is it possible that there is really no relationship between price and acceleration time, and we just happened to choose a sample that led to a slope of -7.1933, by chance?
If there is really no relationship between price and acceleration time, then we would expect a slope (i.e value of \(b_1\) ) equal to 0.
Key Question:
Null Hypothesis: There is no relationship between price and acceleration time, and the slope we observed occurred merely by chance.
Alternative Hypothesis: The slope we observed is due to more than chance, suggesting there is a relationship between price and acceleration time.
Procedure:
ShuffledCars Cars2015 ## create copy of dataset ShuffledCars$Acc060 ShuffledCars$Acc060[sample(1:nrow(ShuffledCars))] | Make | Model | LowPrice | Acc060 | ShuffledAcc060 |
|---|---|---|---|---|
| Chevrolet | Spark | 12.270 | 12.8 | 8.6 |
| Hyundai | Accent | 14.745 | 10.3 | 6.5 |
| Kia | Rio | 13.990 | 9.5 | 7.2 |
| Mitsubishi | Mirage | 12.995 | 12.1 | 7.4 |
| Nissan | Versa Note | 14.180 | 10.9 | 5.4 |
| Dodge | Dart | 16.495 | 9.3 | 8.4 |
Recall this model was fit under an assumption of no relationship between price and acceleration time.
M_Cars_Shuffle lm(data=ShuffledCars, LowPrice~Acc060) summary(M_Cars_Shuffle)## ## Call: ## lm(formula = LowPrice ~ Acc060, data = ShuffledCars) ## ## Residuals: ## Min 1Q Median 3Q Max ## -21.145 -11.306 -3.949 9.605 50.885 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 25.5358 7.5156 3.398 0.000952 *** ## Acc060 0.9162 0.9273 0.988 0.325362 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 15.93 on 108 degrees of freedom ## Multiple R-squared: 0.008957, Adjusted R-squared: -0.0002189 ## F-statistic: 0.9761 on 1 and 108 DF, p-value: 0.3254 ShuffledCars Cars2015 ## create copy of dataset ShuffledCars$Acc060 ShuffledCars$Acc060[sample(1:nrow(ShuffledCars))] | Make | Model | LowPrice | Acc060 | ShuffledAcc060 |
|---|---|---|---|---|
| Chevrolet | Spark | 12.270 | 12.8 | 7.9 |
| Hyundai | Accent | 14.745 | 10.3 | 7.9 |
| Kia | Rio | 13.990 | 9.5 | 7.4 |
| Mitsubishi | Mirage | 12.995 | 12.1 | 6.1 |
| Nissan | Versa Note | 14.180 | 10.9 | 7.2 |
| Dodge | Dart | 16.495 | 9.3 | 5.5 |
Recall this model was fit under an assumption of no relationship between price and acceleration time.
M_Cars_Shuffle lm(data=ShuffledCars, LowPrice~Acc060) summary(M_Cars_Shuffle)## ## Call: ## lm(formula = LowPrice ~ Acc060, data = ShuffledCars) ## ## Residuals: ## Min 1Q Median 3Q Max ## -20.550 -11.017 -3.430 9.464 51.609 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 35.364 7.545 4.687 0.00000814 *** ## Acc060 -0.322 0.931 -0.346 0.73 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 15.99 on 108 degrees of freedom ## Multiple R-squared: 0.001106, Adjusted R-squared: -0.008143 ## F-statistic: 0.1196 on 1 and 108 DF, p-value: 0.7301 ShuffledCars Cars2015 ## create copy of dataset ShuffledCars$Acc060 ShuffledCars$Acc060[sample(1:nrow(ShuffledCars))] | Make | Model | LowPrice | Acc060 | ShuffledAcc060 |
|---|---|---|---|---|
| Chevrolet | Spark | 12.270 | 12.8 | 6.9 |
| Hyundai | Accent | 14.745 | 10.3 | 7.9 |
| Kia | Rio | 13.990 | 9.5 | 10.8 |
| Mitsubishi | Mirage | 12.995 | 12.1 | 6.1 |
| Nissan | Versa Note | 14.180 | 10.9 | 8.4 |
| Dodge | Dart | 16.495 | 9.3 | 7.4 |
Recall this model was fit under an assumption of no relationship between price and acceleration time.
M_Cars_Shuffle lm(data=ShuffledCars, LowPrice~Acc060) summary(M_Cars_Shuffle)## ## Call: ## lm(formula = LowPrice ~ Acc060, data = ShuffledCars) ## ## Residuals: ## Min 1Q Median 3Q Max ## -21.798 -10.745 -3.390 9.009 49.507 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 41.3835 7.5024 5.516 0.000000239 *** ## Acc060 -1.0804 0.9257 -1.167 0.246 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 15.9 on 108 degrees of freedom ## Multiple R-squared: 0.01246, Adjusted R-squared: 0.003311 ## F-statistic: 1.362 on 1 and 108 DF, p-value: 0.2457 ShuffledCars Cars2015 ## create copy of dataset ShuffledCars$Acc060 ShuffledCars$Acc060[sample(1:nrow(ShuffledCars))] | Make | Model | LowPrice | Acc060 | ShuffledAcc060 |
|---|---|---|---|---|
| Chevrolet | Spark | 12.270 | 12.8 | 8.6 |
| Hyundai | Accent | 14.745 | 10.3 | 11.0 |
| Kia | Rio | 13.990 | 9.5 | 6.9 |
| Mitsubishi | Mirage | 12.995 | 12.1 | 10.3 |
| Nissan | Versa Note | 14.180 | 10.9 | 9.8 |
| Dodge | Dart | 16.495 | 9.3 | 6.5 |
Recall this model was fit under an assumption of no relationship between price and acceleration time.
M_Cars_Shuffle lm(data=ShuffledCars, LowPrice~Acc060) summary(M_Cars_Shuffle)## ## Call: ## lm(formula = LowPrice ~ Acc060, data = ShuffledCars) ## ## Residuals: ## Min 1Q Median 3Q Max ## -24.382 -11.808 -3.246 9.664 48.778 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 45.9647 7.4380 6.180 0.0000000116 *** ## Acc060 -1.6576 0.9178 -1.806 0.0737 . ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 15.76 on 108 degrees of freedom ## Multiple R-squared: 0.02932, Adjusted R-squared: 0.02033 ## F-statistic: 3.262 on 1 and 108 DF, p-value: 0.07369 ShuffledCars Cars2015 ## create copy of dataset ShuffledCars$Acc060 ShuffledCars$Acc060[sample(1:nrow(ShuffledCars))] | Make | Model | LowPrice | Acc060 | ShuffledAcc060 |
|---|---|---|---|---|
| Chevrolet | Spark | 12.270 | 12.8 | 8.6 |
| Hyundai | Accent | 14.745 | 10.3 | 7.7 |
| Kia | Rio | 13.990 | 9.5 | 7.7 |
| Mitsubishi | Mirage | 12.995 | 12.1 | 6.8 |
| Nissan | Versa Note | 14.180 | 10.9 | 7.9 |
| Dodge | Dart | 16.495 | 9.3 | 10.9 |
Recall this model was fit under an assumption of no relationship between price and acceleration time.
M_Cars_Shuffle lm(data=ShuffledCars, LowPrice~Acc060) summary(M_Cars_Shuffle)## ## Call: ## lm(formula = LowPrice ~ Acc060, data = ShuffledCars) ## ## Residuals: ## Min 1Q Median 3Q Max ## -20.469 -11.188 -3.441 8.841 50.951 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 37.3890 7.5361 4.961 0.00000262 *** ## Acc060 -0.5771 0.9299 -0.621 0.536 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 15.97 on 108 degrees of freedom ## Multiple R-squared: 0.003554, Adjusted R-squared: -0.005672 ## F-statistic: 0.3852 on 1 and 108 DF, p-value: 0.5361 b1 Cars_M_A060$coef[2] ## record value of b1 from actual data ## perform simulation b1Sim rep(NA, 10000) ## vector to hold results ShuffledCars Cars2015 ## create copy of dataset for (i in 1:10000) #randomly shuffle acceleration times ShuffledCars$Acc060 ShuffledCars$Acc060[sample(1:nrow(ShuffledCars))] ShuffledCars_M lm(data=ShuffledCars, LowPrice ~ Acc060) #fit model to shuffled data b1Sim[i] ShuffledCars_M$coef[2] ## record b1 from shuffled model > Cars_A060SimulationResults data.frame(b1Sim) #save results in dataframe b1 Cars_M_A060$coef[2] ## record value of b1 from actual data Cars_A060SimulationResultsPlot ggplot(data=Cars_A060SimulationResults, aes(x=b1Sim)) + geom_histogram(fill="lightblue", color="white") + geom_vline(xintercept=c(b1, -1*b1), color="red") + xlab("Simulated Value of b1") + ylab("Frequency") + ggtitle("Distribution of b1 under assumption of no relationship") Cars_A060SimulationResultsPlot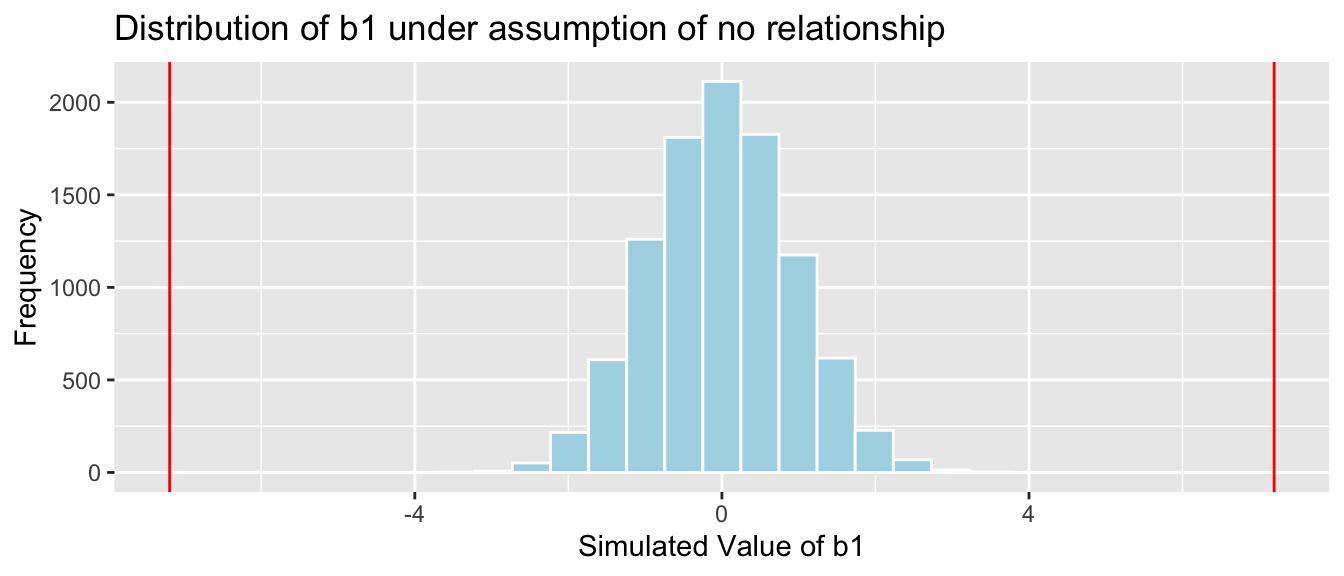
It is extremely unlikely that we would observe a value of \(b_1\) as extreme as -7.1933 by chance, if there is really no relationship between price and acceleration time.
Proportion of simulations resulting in simulation value of \(b_2\) more extreme than -7.1933.
mean(abs(b1Sim) > abs(b1))The probability of observing a value of \(b_1\) as extreme as -7.1933 by chance, when there is no relationship between location and mercury level practically zero.
There is very strong evidence of a relationship between price and acceleration time.
q.025 quantile(Cars_Bootstrap_Results_Acc060$b1, .025) q.975 quantile(Cars_Bootstrap_Results_Acc060$b1, .975) Cars_Acc060_B_Slope_Plot + geom_vline(xintercept=c(q.025, q.975), col="red")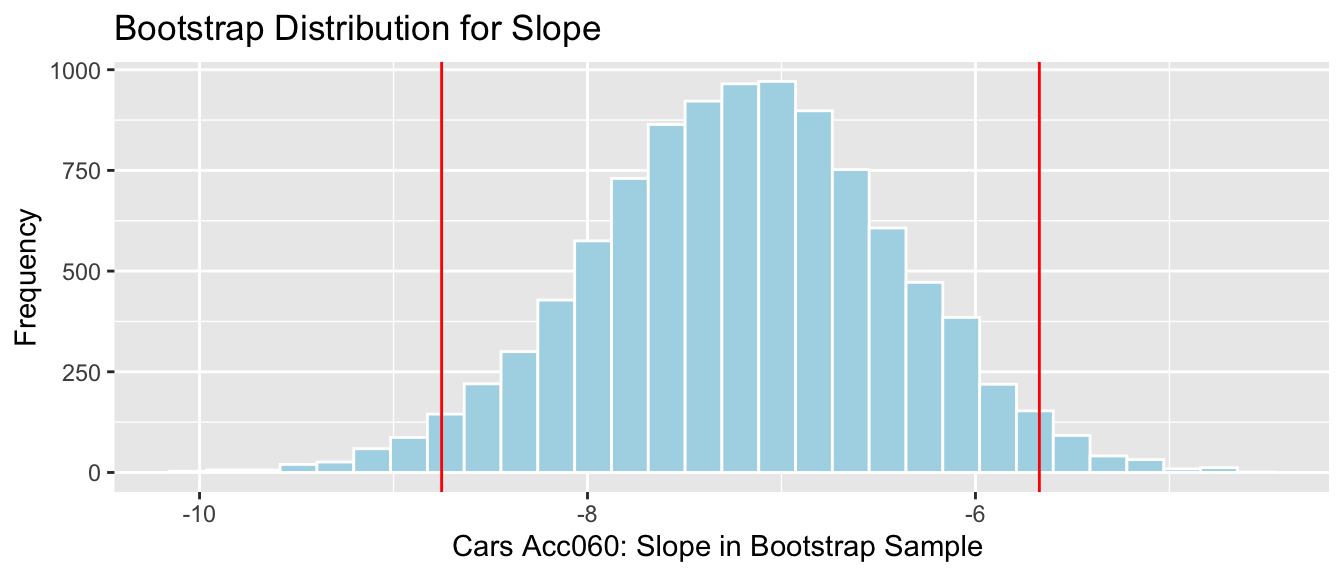
We are 95% confident that the average price of a new 2015 car decreases between -8.75 and -5.67 thousand dollars for each additional second it takes to accelerate from 0 to 60 mph.
ggplot(data=Cars2015, aes(x=Size, y=LowPrice, fill=Size)) + geom_boxplot() + geom_jitter() + coord_flip()
Cars2015 %>% group_by(Size) %>% summarize(MeanPrice = mean(LowPrice), StDevPrice=sd(LowPrice), N=n())## # A tibble: 3 x 4 ## Size MeanPrice StDevPrice N ## ## 1 Large 42.3 17.9 29 ## 2 Midsized 33.2 12.0 34 ## 3 Small 26.7 14.4 47 Cars_M_Size = lm(data=Cars2015, LowPrice~Size) summary(Cars_M_Size)## ## Call: ## lm(formula = LowPrice ~ Size, data = Cars2015) ## ## Residuals: ## Min 1Q Median 3Q Max ## -20.516 -11.190 -4.005 9.064 57.648 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 42.311 2.737 15.460 < 0.0000000000000002 *** ## SizeMidsized -9.098 3.725 -2.442 0.0162 * ## SizeSmall -15.659 3.480 -4.499 0.0000174 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 14.74 on 107 degrees of freedom ## Multiple R-squared: 0.1593, Adjusted R-squared: 0.1436 ## F-statistic: 10.14 on 2 and 107 DF, p-value: 0.00009271Unfortunately, none of these measure whether there is an overall relationship between price and size.
Recall that the ANOVA F-statistic combines information from all of the groups. Thus, it can be used to assess the strength of evidence of differences.
Cars_A_Size aov(data=Cars2015, LowPrice~Size) summary(Cars_A_Size)## Df Sum Sq Mean Sq F value Pr(>F) ## Size 2 4405 2202.7 10.14 0.0000927 *** ## Residuals 107 23242 217.2 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Null Hypothesis: There is no relationship between price and car size.
Alternative Hypothesis: There is a relationship between price and car size.
Key Question: How likely is it that we would have obtained an F-statistic as extreme as 10.14 by chance, if there is really no relationship between price and size?
We’ll simulate situations where there is no relationship between size and price, and see how often we observe an F-statistic as extreme as 10.14.
Procedure:
ShuffledCars Cars2015 ## create copy of dataset ShuffledCars$Size ShuffledCars$Size[sample(1:nrow(ShuffledCars))] | Make | Model | LowPrice | Size | ShuffledSize |
|---|---|---|---|---|
| Chevrolet | Spark | 12.270 | Small | Large |
| Hyundai | Accent | 14.745 | Small | Large |
| Kia | Rio | 13.990 | Small | Large |
| Mitsubishi | Mirage | 12.995 | Small | Small |
| Nissan | Versa Note | 14.180 | Small | Midsized |
| Dodge | Dart | 16.495 | Small | Midsized |
Recall this model was fit under an assumption of no relationship between price and size.
ggplot(data=ShuffledCars, aes(x=Size, y=LowPrice, fill=Size)) + geom_boxplot() + geom_jitter() + coord_flip() + ggtitle("Shuffled Cars")
Cars_A_Size_Shuffle aov(data=ShuffledCars, LowPrice~Size) summary(Cars_A_Size_Shuffle)## Df Sum Sq Mean Sq F value Pr(>F) ## Size 2 231 115.6 0.451 0.638 ## Residuals 107 27417 256.2 ShuffledCars Cars2015 ## create copy of dataset ShuffledCars$Size ShuffledCars$Size[sample(1:nrow(ShuffledCars))] | Make | Model | LowPrice | Size | ShuffledSize |
|---|---|---|---|---|
| Chevrolet | Spark | 12.270 | Small | Midsized |
| Hyundai | Accent | 14.745 | Small | Small |
| Kia | Rio | 13.990 | Small | Midsized |
| Mitsubishi | Mirage | 12.995 | Small | Small |
| Nissan | Versa Note | 14.180 | Small | Small |
| Dodge | Dart | 16.495 | Small | Small |
Recall this model was fit under an assumption of no relationship between price and size.
ggplot(data=ShuffledCars, aes(x=Size, y=LowPrice, fill=Size)) + geom_boxplot() + geom_jitter() + coord_flip() + ggtitle("Shuffled Cars")
Cars_A_Size_Shuffle aov(data=ShuffledCars, LowPrice~Size) summary(Cars_A_Size_Shuffle)## Df Sum Sq Mean Sq F value Pr(>F) ## Size 2 1134 566.8 2.287 0.106 ## Residuals 107 26514 247.8 ShuffledCars Cars2015 ## create copy of dataset ShuffledCars$Size ShuffledCars$Size[sample(1:nrow(ShuffledCars))] | Make | Model | LowPrice | Size | ShuffledSize |
|---|---|---|---|---|
| Chevrolet | Spark | 12.270 | Small | Large |
| Hyundai | Accent | 14.745 | Small | Midsized |
| Kia | Rio | 13.990 | Small | Small |
| Mitsubishi | Mirage | 12.995 | Small | Small |
| Nissan | Versa Note | 14.180 | Small | Large |
| Dodge | Dart | 16.495 | Small | Midsized |
Recall this model was fit under an assumption of no relationship between price and size.
ggplot(data=ShuffledCars, aes(x=Size, y=LowPrice, fill=Size)) + geom_boxplot() + geom_jitter() + coord_flip() + ggtitle("Shuffled Cars")
Cars_A_Size_Shuffle aov(data=ShuffledCars, LowPrice~Size) summary(Cars_A_Size_Shuffle)## Df Sum Sq Mean Sq F value Pr(>F) ## Size 2 128 64.21 0.25 0.78 ## Residuals 107 27519 257.19 ShuffledCars Cars2015 ## create copy of dataset ShuffledCars$Size ShuffledCars$Size[sample(1:nrow(ShuffledCars))] | Make | Model | LowPrice | Size | ShuffledSize |
|---|---|---|---|---|
| Chevrolet | Spark | 12.270 | Small | Large |
| Hyundai | Accent | 14.745 | Small | Midsized |
| Kia | Rio | 13.990 | Small | Large |
| Mitsubishi | Mirage | 12.995 | Small | Large |
| Nissan | Versa Note | 14.180 | Small | Small |
| Dodge | Dart | 16.495 | Small | Midsized |
Recall this model was fit under an assumption of no relationship between price and size.
ggplot(data=ShuffledCars, aes(x=Size, y=LowPrice, fill=Size)) + geom_boxplot() + geom_jitter() + coord_flip() + ggtitle("Shuffled Cars")
Cars_A_Size_Shuffle aov(data=ShuffledCars, LowPrice~Size) summary(Cars_A_Size_Shuffle)## Df Sum Sq Mean Sq F value Pr(>F) ## Size 2 46 22.86 0.089 0.915 ## Residuals 107 27602 257.96 ShuffledCars Cars2015 ## create copy of dataset ShuffledCars$Size ShuffledCars$Size[sample(1:nrow(ShuffledCars))] | Make | Model | LowPrice | Size | ShuffledSize |
|---|---|---|---|---|
| Chevrolet | Spark | 12.270 | Small | Midsized |
| Hyundai | Accent | 14.745 | Small | Small |
| Kia | Rio | 13.990 | Small | Small |
| Mitsubishi | Mirage | 12.995 | Small | Small |
| Nissan | Versa Note | 14.180 | Small | Large |
| Dodge | Dart | 16.495 | Small | Small |
Recall this model was fit under an assumption of no relationship between price and size.
ggplot(data=ShuffledCars, aes(x=Size, y=LowPrice, fill=Size)) + geom_boxplot() + geom_jitter() + coord_flip() + ggtitle("Shuffled Cars")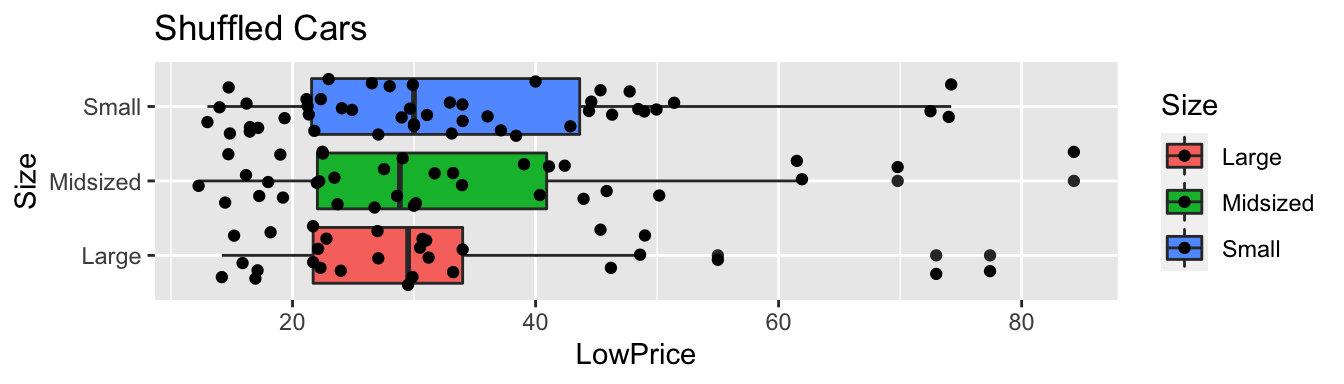
Cars_A_Size_Shuffle aov(data=ShuffledCars, LowPrice~Size) summary(Cars_A_Size_Shuffle)## Df Sum Sq Mean Sq F value Pr(>F) ## Size 2 22 10.9 0.042 0.959 ## Residuals 107 27626 258.2 Fstat summary(Cars_M_Size)$fstatistic[1] ## record value of F-statistic from actual data ## perform simulation FSim rep(NA, 10000) ## vector to hold results ShuffledCars Cars2015 ## create copy of dataset for (i in 1:10000) #randomly shuffle acceleration times ShuffledCars$Size ShuffledCars$Size[sample(1:nrow(ShuffledCars))] ShuffledCars_M lm(data=ShuffledCars, LowPrice ~ Size) #fit model to shuffled data FSim[i] summary(ShuffledCars_M)$fstatistic[1] ## record F from shuffled model > CarSize_SimulationResults data.frame(FSim) #save results in dataframe CarSize_SimulationResults_Plot ggplot(data=CarSize_SimulationResults, aes(x=FSim)) + geom_histogram(fill="lightblue", color="white") + geom_vline(xintercept=c(Fstat), color="red") + xlab("Simulated Value of F") + ylab("Frequency") + ggtitle("Distribution of F under assumption of no relationship") CarSize_SimulationResults_Plot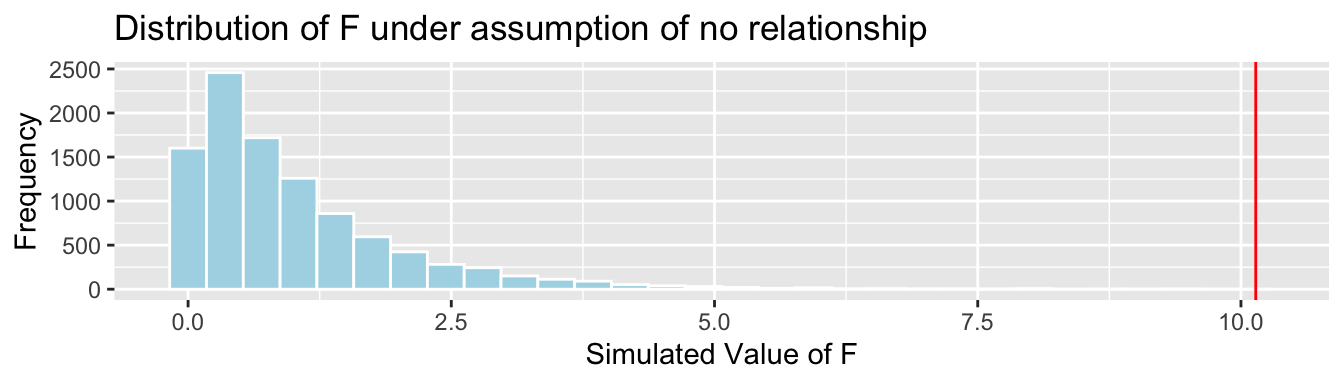
mean(FSim > Fstat)The data provide strong evidence of a relationship between price and size.
Now that we have evidence that car price is related to size, we might want to know which sizes differ from each other.
Is there evidence of a difference in average price between…
a) large and midsized cars?
b) large and small cars?
c) small and midsized cars?
Thus, we can answer each question by looking at the appropriate regression coefficient.
a) large and midsized cars? ( \(b_1\) )
b) large and small cars? ( \(b_2\) )
c) small and midsized cars? ( \(b_1-b_2\) )
We’ll simulate situations where there is no relationship between size and price, and see how often we observe results for \(b_1\) , \(b_2\) , and \(b_1-b_2\) as extreme as we did in the actual data.
Procedure:
b1 Cars_M_Size$coefficients[2] #record b1 from actual data b2 Cars_M_Size$coefficients[3] #record b2 from actual data ## perform simulation b1Sim rep(NA, 10000) ## vector to hold results b2Sim rep(NA, 10000) ## vector to hold results ShuffledCars Cars2015 ## create copy of dataset for (i in 1:10000) #randomly shuffle acceleration times ShuffledCars$Size ShuffledCars$Size[sample(1:nrow(ShuffledCars))] ShuffledCars_M lm(data=ShuffledCars, LowPrice ~ Size) #fit model to shuffled data b1Sim[i] ShuffledCars_M$coefficients[2] ## record b1 from shuffled model b2Sim[i] ShuffledCars_M$coefficients[3] ## record b2 from shuffled model > Cars_Size2_SimulationResults data.frame(b1Sim, b2Sim) #save results in dataframe Cars_Size2_SimulationResultsPlot_b1 ggplot(data=Cars_Size2_SimulationResults, aes(x=b1Sim)) + geom_histogram(fill="lightblue", color="white") + geom_vline(xintercept=c(b1, -1*b1), color="red") + xlab("Simulated Value of b1") + ylab("Frequency") + ggtitle("Large vs Midsize Cars: Distribution of b1 under assumption of no relationship") Cars_Size2_SimulationResultsPlot_b1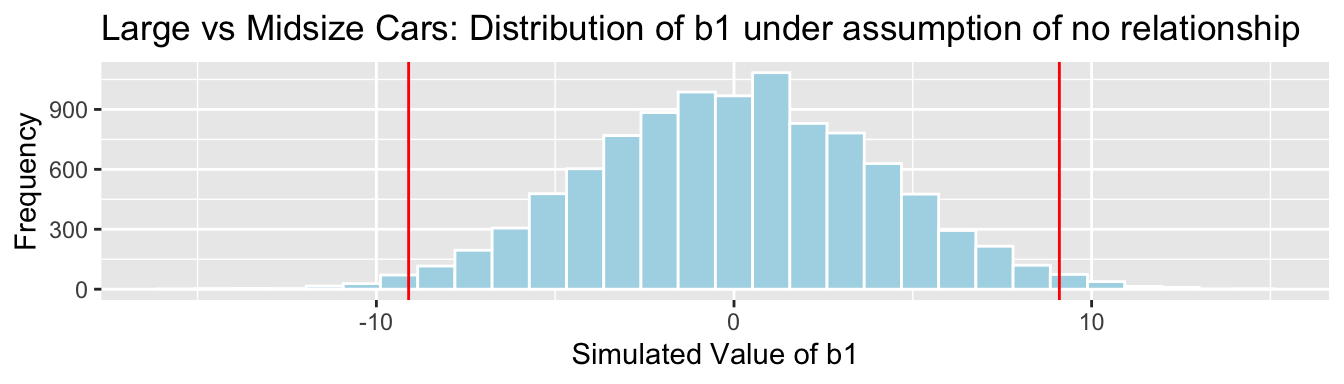
mean(abs(b1Sim)>abs(b1))## [1] 0.0219 Cars_Size2_SimulationResultsPlot_b2 ggplot(data=Cars_Size2_SimulationResults, aes(x=b2Sim)) + geom_histogram(fill="lightblue", color="white") + geom_vline(xintercept=c(b2, -1*b2), color="red") + xlab("Simulated Value of b2") + ylab("Frequency") + ggtitle("Large vs Small Cars: Distribution of b2 under assumption of no relationship") Cars_Size2_SimulationResultsPlot_b2
mean(abs(b2Sim)>abs(b2)) Cars_Size2_SimulationResultsPlot_b1_b2 ggplot(data=Cars_Size2_SimulationResults, aes(x=b1Sim-b2Sim)) + geom_histogram(fill="lightblue", color="white") + geom_vline(xintercept=c(b1-b2, -1*(b1-b2)), color="red") + xlab("Simulated Value of b1-b2") + ylab("Frequency") + ggtitle("Small vs Midsize Cars: Distribution of b1-b2 under assumption of no relationship") Cars_Size2_SimulationResultsPlot_b1_b2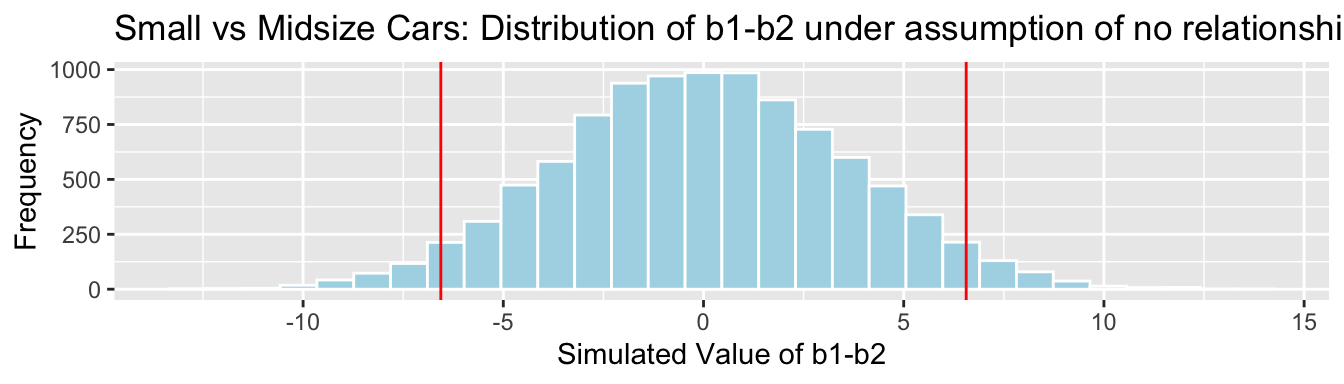
mean(abs(b1Sim-b2Sim)>abs(b1-b2))## [1] 0.0678| Comparison | Coefficient | p-value | Evidence of Difference |
|---|---|---|---|
| large vs midsize | \(b_1\) | 0.0219 | Some evidence |
| large vs small | \(b_2\) | 0 | Strong evidence |
| small vs midsize | \(b_1-b_2\) | 0.0678 | No evidence |
When testing for differences between more than two groups:
ggplot(data=Bears_Subset, aes(y=Weight, x=Season, fill=Season)) + geom_boxplot() + geom_jitter() + coord_flip()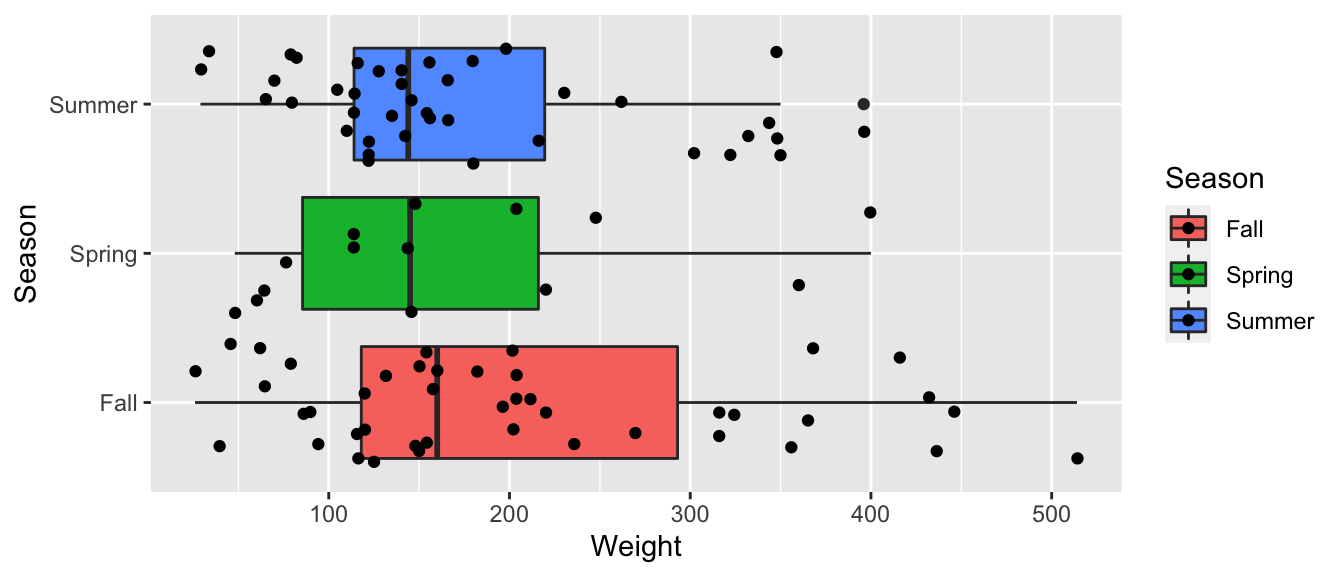
Bears_M_Season lm(data=Bears_Subset, Weight~Season) summary(Bears_M_Season)## ## Call: ## lm(formula = Weight ~ Season, data = Bears_Subset) ## ## Residuals: ## Min 1Q Median 3Q Max ## -178.84 -79.84 -29.02 54.98 309.16 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 204.84 17.16 11.939 Bears_A_Season aov(data=Bears_Subset, Weight~Season) summary(Bears_A_Season)## Df Sum Sq Mean Sq F value Pr(>F) ## Season 2 24699 12350 0.976 0.381 ## Residuals 94 1189818 12658Null Hypothesis: Mean weight of bears is the same in each season.
Alternative Hypothesis: Mean weight of bears differs between seasons.
Key Question: What is the probability of observing an F-statistic as extreme as 0.976 if there is really no relationship between weight and season?
We’ll simulate situations where there is no relationship between size and price, and see how often we observe an F-statistic as extreme as 0.976.
Procedure:
Fstat summary(Bears_M_Season)$fstatistic[1] ## record value of F-statistic from actual data ## perform simulation FSim rep(NA, 10000) ## vector to hold results ShuffledBears Bears_Subset ## create copy of dataset for (i in 1:10000) #randomly shuffle acceleration times ShuffledBears$Season ShuffledBears$Season[sample(1:nrow(ShuffledBears))] ShuffledBears_M lm(data=ShuffledBears, Weight ~ Season) #fit model to shuffled data FSim[i] summary(ShuffledBears_M)$fstatistic[1] ## record F from shuffled model > Bears_Seasons_SimulationResults data.frame(FSim) #save results in dataframe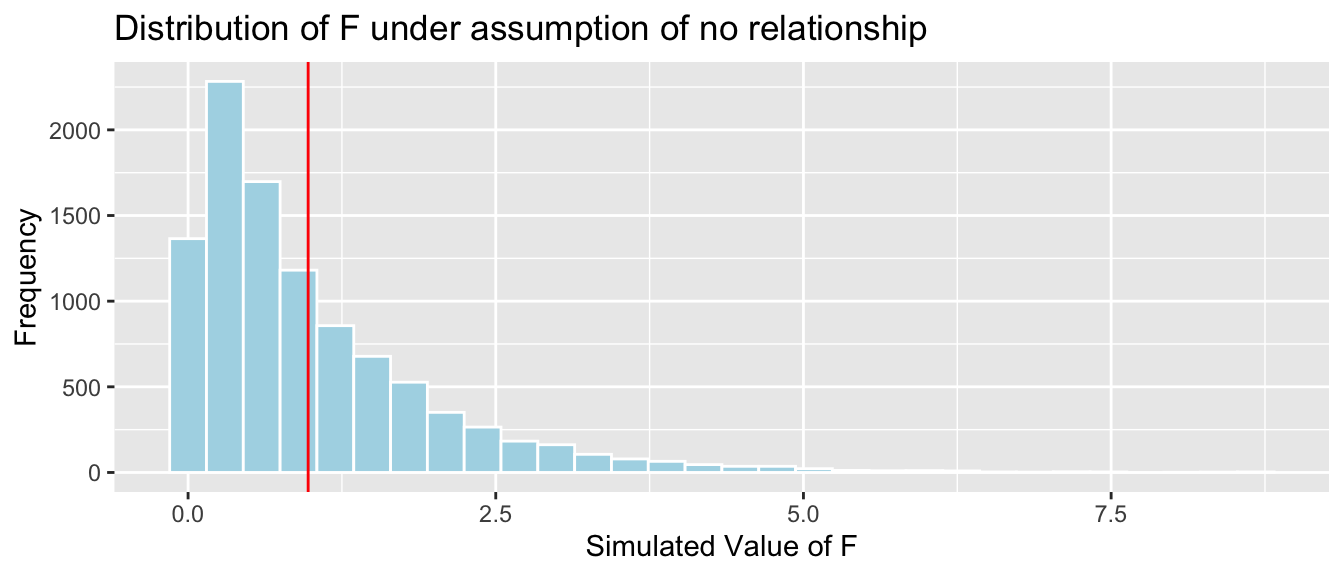
mean(FSim > Fstat)## [1] 0.3705It is not at all unusual to observe an F-statistic as extreme or more extreme than we did if there is really no relationship between weight and season.
There is no evidence that average bear weights differ between seasons.
Bears_Season_Table Bears_Subset %>% group_by(Season) %>% summarize(MeanWeight = mean(Weight), StDevWeight = sd(Weight), N=n()) kable(Bears_Season_Table)| Season | MeanWeight | StDevWeight | N |
|---|---|---|---|
| Fall | 204.8372 | 125.71414 | 43 |
| Spring | 167.5714 | 108.74155 | 14 |
| Summer | 175.0250 | 97.70796 | 40 |
The data do show differences in average weight between seasons. It’s just that we can’t rule out the possibility that these differences are due to chance alone.
In the previous sections, we’ve used simulation to obtain confidence intervals and perform hypothesis tests.
In fact, R provides intervals and tests directly, without performing simulations. These are calculated using theory-based approximation formulas that often (but not always) lead to the same conculsions as the simulation-based methods.
In this section, we’ll look at how to obtain these tests and intervals in R.
In Chapter 5, we’ll explore more of the reasoning behind these approaches.
ggplot(data=FloridaLakes, aes(x=Location, y=AvgMercury, fill=Location)) + geom_boxplot() + geom_jitter() + ggtitle("Mercury Levels in Florida Lakes") + xlab("Location") + ylab("Mercury Level") + theme(axis.text.x = element_text(angle = 90)) + coord_flip()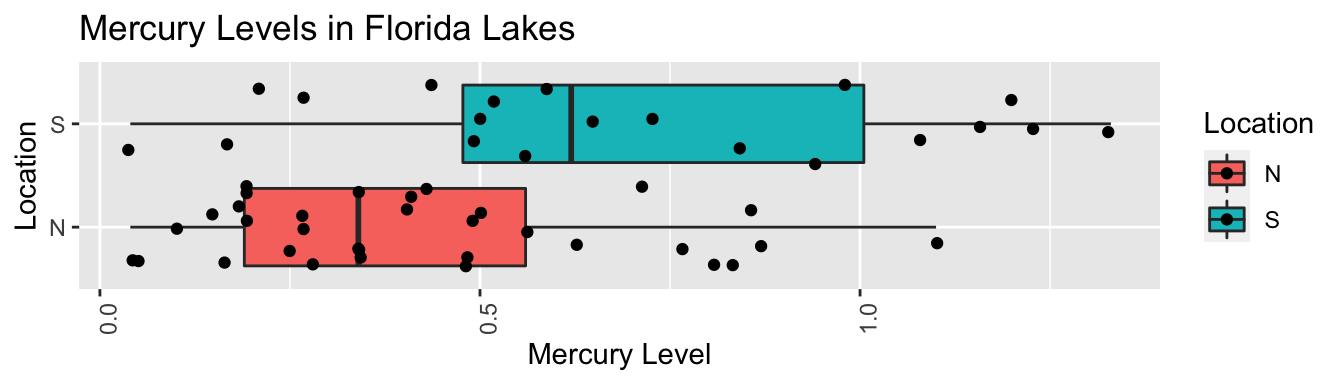
FloridaLakes %>% group_by(Location) %>% summarize(MeanHg=mean(AvgMercury), StDevHg=sd(AvgMercury), N=n())## # A tibble: 2 x 4 ## Location MeanHg StDevHg N ## ## 1 N 0.425 0.270 33 ## 2 S 0.696 0.384 20Null Hypothesis: There is no difference in mean mercury level between lakes in Northern Florida and Southern Florida. This is equivalent to saying \(\beta_1=0\) .
Alternative Hypothesis: The mean mercury level differs between lakes in Northern and Southern Florida. This is equivalent to saying \(\beta_1\neq0\) .
Lakes_M lm(data=FloridaLakes, AvgMercury ~ Location) summary(Lakes_M)## ## Call: ## lm(formula = AvgMercury ~ Location, data = FloridaLakes) ## ## Residuals: ## Min 1Q Median 3Q Max ## -0.65650 -0.23455 -0.08455 0.24350 0.67545 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 0.42455 0.05519 7.692 0.000000000441 *** ## LocationS 0.27195 0.08985 3.027 0.00387 ** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.3171 on 51 degrees of freedom ## Multiple R-squared: 0.1523, Adjusted R-squared: 0.1357 ## F-statistic: 9.162 on 1 and 51 DF, p-value: 0.003868The quantity Pr(>|t|) in the coefficients table contains p-values pertaining to the test of the null hypothesis that that parameter is 0.
summary(Lakes_M)$coefficients## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 0.4245455 0.05519303 7.692012 0.0000000004414948 ## LocationS 0.2719545 0.08984774 3.026838 0.0038681284084829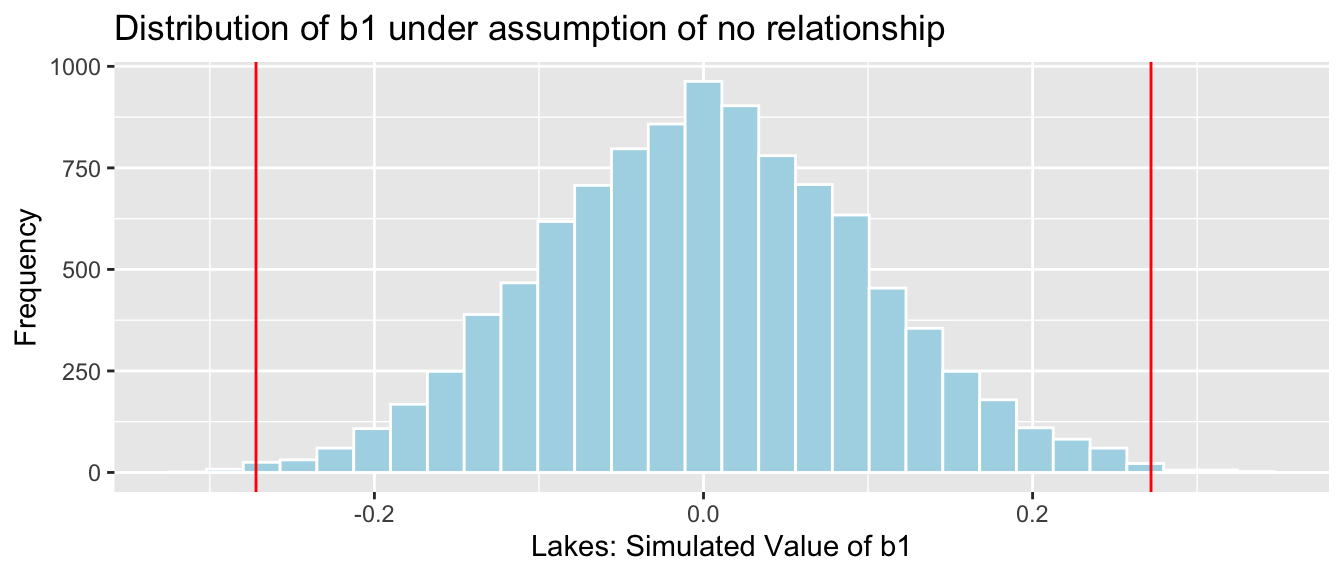
## [1] 0.0031 summary(Lakes_M)$coefficients## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 0.4245455 0.05519303 7.692012 0.0000000004414948 ## LocationS 0.2719545 0.08984774 3.026838 0.0038681284084829The confint() command returns “theory-based” confidence intervals for model parameters \(\beta_0\) and \(\beta_1\) .
confint(Lakes_M, level = 0.95)## 2.5 % 97.5 % ## (Intercept) 0.31374083 0.5353501 ## LocationS 0.09157768 0.4523314We are 95% confident that the mean mercury level in northern lakes is between 0.31 and 0.54 ppm.
We are 95% confident that the mean mercury level in southern lakes is between 0.09 and 0.45 ppm higher than in northern lakes.
## 2.5% 97.5% ## 0.08095682 0.46122992 NS_Lakes_Bootstrap_Plot_b1 + geom_vline(xintercept = c(q.025, q.975), color="red")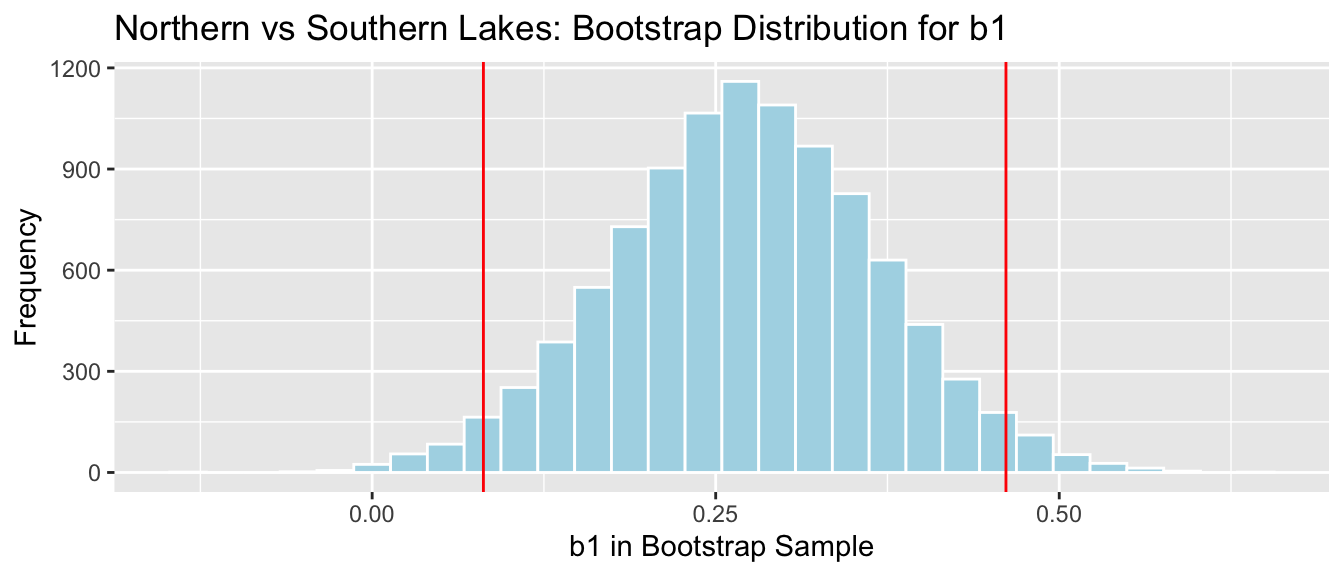
We are 95% confident the average mercury level in Southern Lakes is between 0.08 and 0.46 ppm higher than in Northern Florida.
summary(Cars_M_A060)$coefficients## Estimate Std. Error t value ## (Intercept) 89.903579 5.0523246 17.79450 ## Acc060 -7.193339 0.6234005 -11.53887 ## Pr(>|t|) ## (Intercept) 0.000000000000000000000000000000000688871 ## Acc060 0.000000000000000000014854277120867462701The p-value of \(\approx 0\) on the Acc060 line provides strong evidence against the null hypothesis that \(\beta_1=0\) . (Recall, \(\beta_1\) represents the slope of the regression line pertaining to all cars.) Thus, there is strong evidence of a relationship between car price and acceleration time.
The p-value of \(\approx 0\) on the (Intercept) line provides strong evidence against the null hypothesis that \(\beta_0=0\) . This is not meaningful, since the intercept has no meaningful interpretation.
Cars_A060SimulationResultsPlot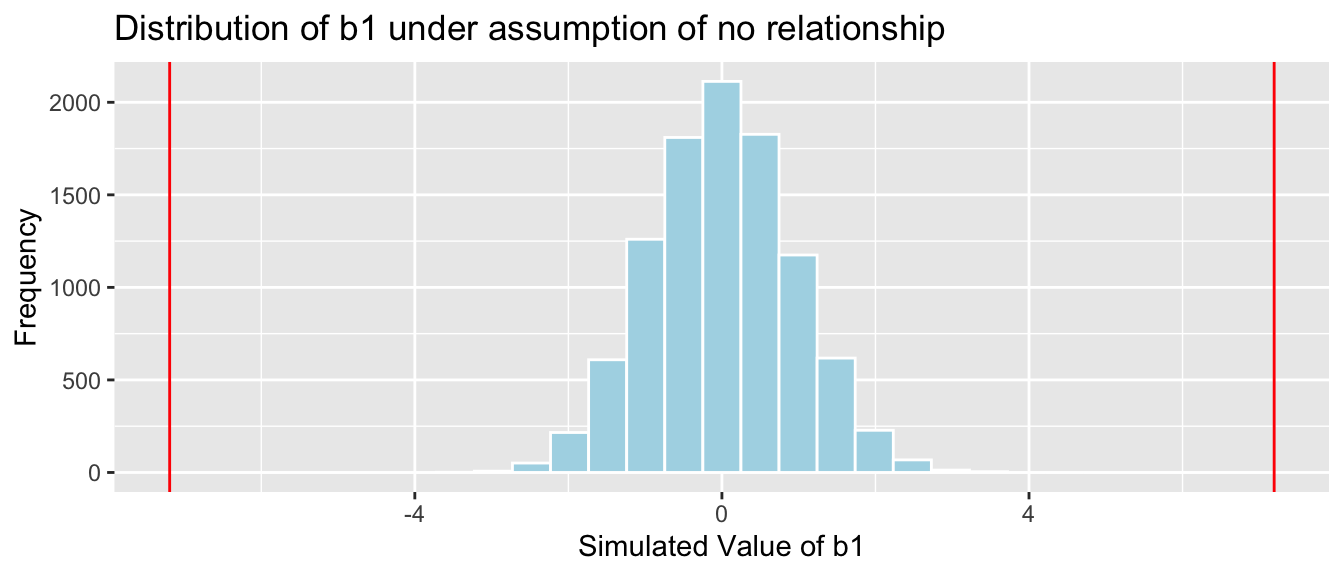
mean(abs(Cars_A060SimulationResults$b1Sim) > abs(coef(Cars_M_A060)[2])) confint(Cars_M_A060)## 2.5 % 97.5 % ## (Intercept) 79.888995 99.918163 ## Acc060 -8.429027 -5.957651We are 95% confident that the mean price of a car decreases between 5.96 and 8.43 thousand dollars for each additional second it takes to accelerate from 0 to 60 mph.
q.025 quantile(Cars_Bootstrap_Results_Acc060$b1, .025) q.975 quantile(Cars_Bootstrap_Results_Acc060$b1, .975) Cars_Acc060_B_Slope_Plot + geom_vline(xintercept=c(q.025, q.975), col="red")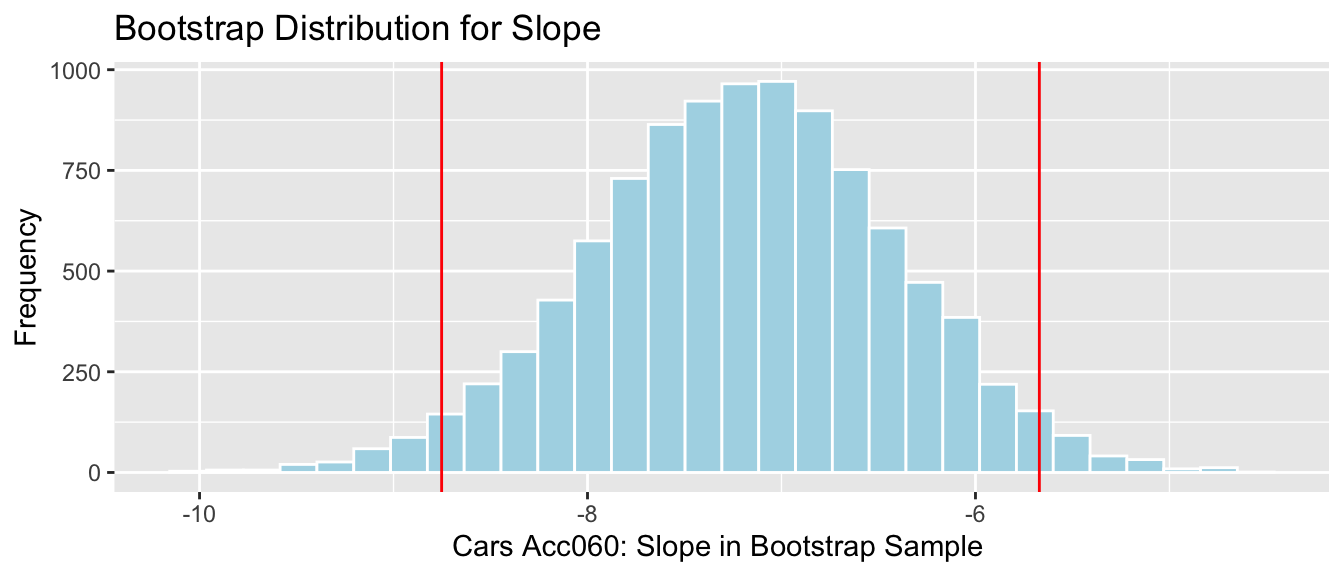
We are 95% confident that the average price of a new 2015 car decreases between -8.75 and -5.67 thousand dollars for each additional second it takes to accelerate from 0 to 60 mph.
Recall this model was fit under an assumption of no relationship between price and size.
ggplot(data=Cars2015, aes(x=Size, y=LowPrice, fill=Size)) + geom_boxplot() + geom_jitter() + coord_flip() + ggtitle("Shuffled Cars")
Null Hypothesis: There are no differences in average price between small, medium, and large cars.
Alternative Hypothesis: There are differences in average price between the different car sizes.
summary(Cars_A_Size)## Df Sum Sq Mean Sq F value Pr(>F) ## Size 2 4405 2202.7 10.14 0.0000927 *** ## Residuals 107 23242 217.2 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The p-value of 0.0000927 provides strong evidence against the null hypothesis. There is evidence of differences in average price between types of cars.
CarSize_SimulationResults_Plot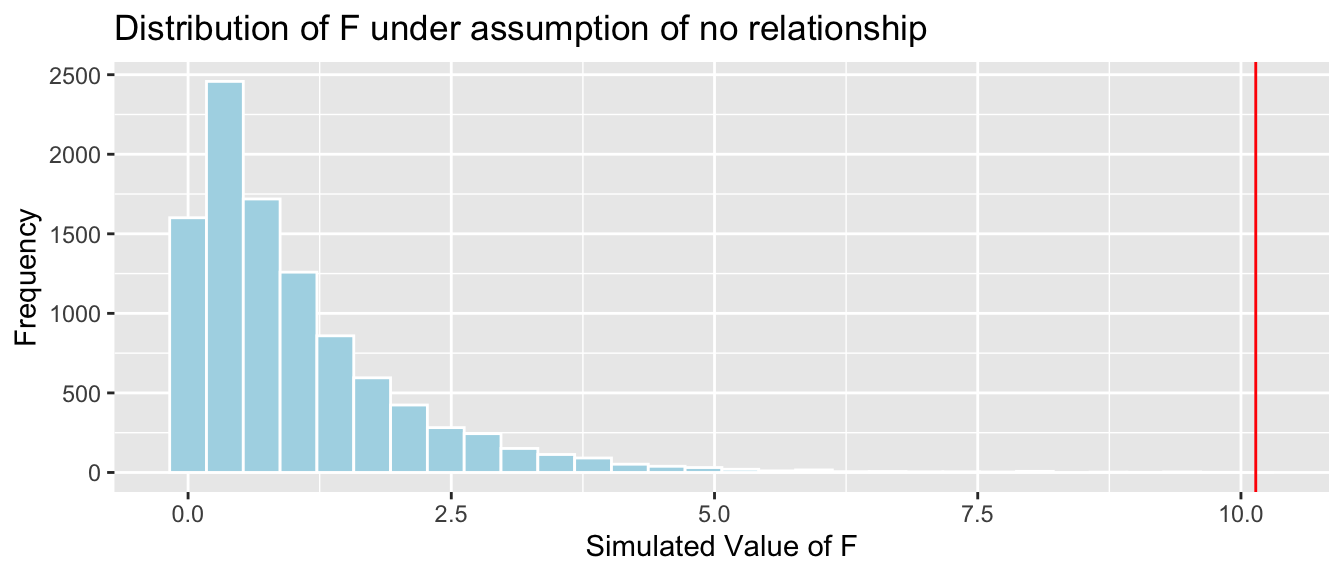
Having established that some sizes differ from one-another, we can obtain p-values for tests comparing individual sizes using the pairwise.t.test() command.
pairwise.t.test(Cars2015$LowPrice, Cars2015$Size, p.adj="none")## ## Pairwise comparisons using t tests with pooled SD ## ## data: Cars2015$LowPrice and Cars2015$Size ## ## Large Midsized ## Midsized 0.016 - ## Small 0.000017 0.051 ## ## P value adjustment method: noneWe should account for performing multiple tests via the Bonferroni correction.
| Comparison | Coefficient | p-value | Evidence of Difference |
|---|---|---|---|
| large vs midsize | \(b_1\) | 0.0219 | Some evidence |
| large vs small | \(b_2\) | 0 | Strong evidence |
| small vs midsize | \(b_1-b_2\) | 0.0678 | No evidence |
ggplot(data=Bears_Subset, aes(y=Weight, x=Season, fill=Season)) + geom_boxplot() + geom_jitter() + coord_flip()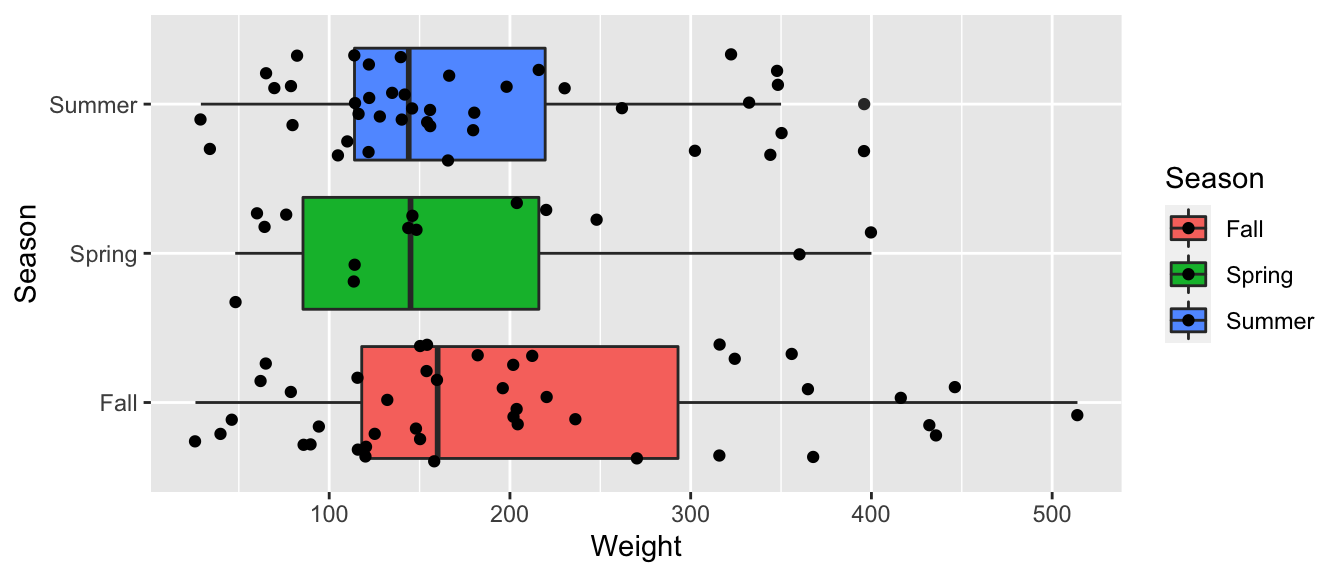
Null Hypothesis: Mean weight of bears is the same in each season.
Alternative Hypothesis: Mean weight of bears differs between seasons.
Bears_A_Season aov(data=Bears_Subset, Weight~Season) summary(Bears_A_Season)## Df Sum Sq Mean Sq F value Pr(>F) ## Season 2 24699 12350 0.976 0.381 ## Residuals 94 1189818 12658The large p-value means there is no evidence of differences in average weight between seasons.
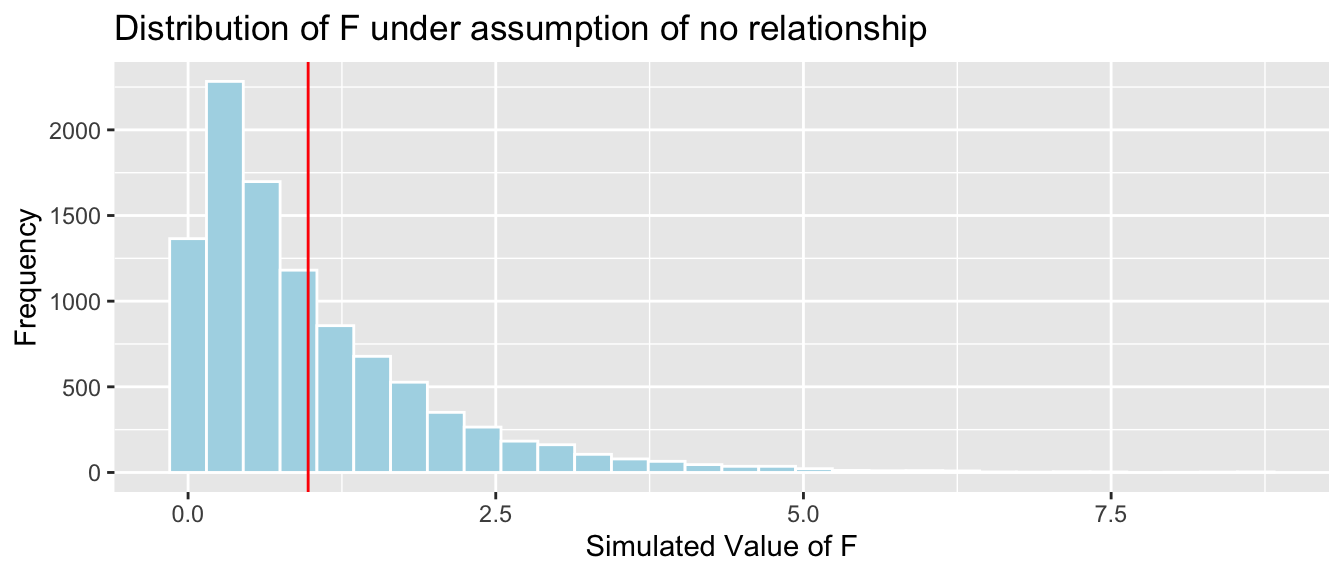
## [1] 0.3705 summary(Bear_M_Age_Sex_Int)## ## Call: ## lm(formula = Weight ~ Age * Sex, data = Bears_Subset) ## ## Residuals: ## Min 1Q Median 3Q Max ## -207.583 -38.854 -9.574 23.905 174.802 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 70.4322 17.7260 3.973 0.000219 *** ## Age 3.2381 0.3435 9.428 0.000000000000765 *** ## Sex2 -31.9574 35.0314 -0.912 0.365848 ## Age:Sex2 -1.0350 0.6237 -1.659 0.103037 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 70.18 on 52 degrees of freedom ## (41 observations deleted due to missingness) ## Multiple R-squared: 0.6846, Adjusted R-squared: 0.6664 ## F-statistic: 37.62 on 3 and 52 DF, p-value: 0.0000000000004552| Sex | Pred. Weight |
|---|---|
| M | \(b_0 + b_1 \times\text\) |
| F | \((b_0 + b_2) + (b_1 + b_3) \times\text\) |
Interpretations:
\(b_0\) : expected weight of a male bear at birth (caution:extrapolation)
\(b_1\) : expected weight gain per month for male bears
\(b_2\) : expected difference in weight between female and male bears at birth (caution:extrapolation)
\(b_3\) : expected difference in monthly weight gain for female bears, compared to male bears
summary(Bears_M_Age_Sex_Int)$coefficients## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 70.432231 17.7259878 3.9733882 0.0002192800056185228 ## Age 3.238137 0.3434770 9.4275225 0.0000000000007646023 ## Sex2 -31.957367 35.0314208 -0.9122487 0.3658478717994073648 ## Age:Sex2 -1.035010 0.6236905 -1.6594923 0.1030365993379950412 confint(Bears_M_Age_Sex_Int)## 2.5 % 97.5 % ## (Intercept) 34.862434 106.002027 ## Age 2.548900 3.927374 ## Sex2 -102.253056 38.338322 ## Age:Sex2 -2.286536 0.216517The average weight gain per month for male bears is represented by \(b_1\) .
## 2.5% 97.5% ## 2.360746 5.970272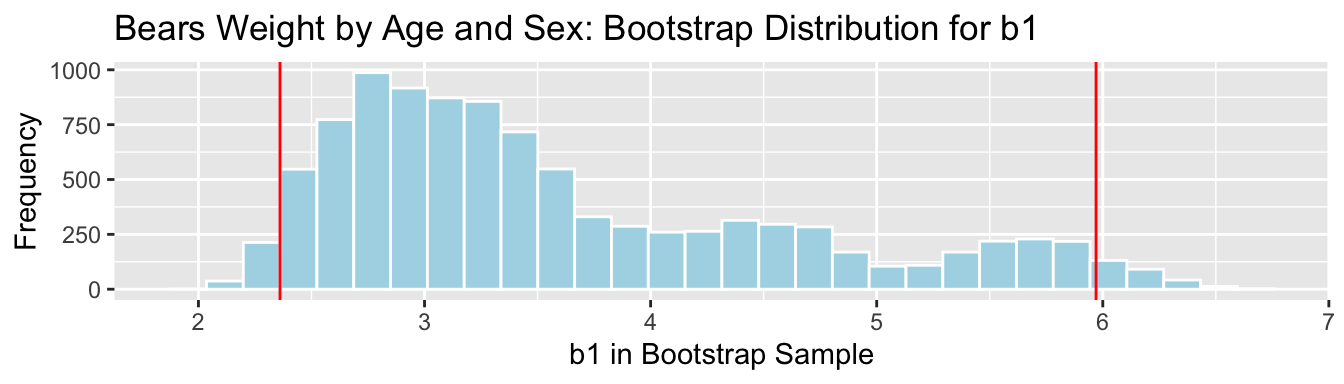
We are 95% confident that male bears gain between 2.36 and 5.97 pounds per month, on average.
The simulation-based and theory-based methods disagree! The theory-based methods only work when the sampling distribution is symmetric and bell-shaped.
Performing responsible statistical inference requires understanding what p-values do and do not tell us, and how they should and should not be interpreted.
A travelor lives in New York and wants to fly to Chicago. They consider flying out of two New York airports:
We have data on the times of flights from both airports to Chicago’s O’Hare airport from 2013 (more than 14,000 flights).
Assuming these flights represent a random sample of all flights from these airports to Chicago, consider how the traveler might use this information to decide which airport to fly out of.
library(nycflights13) data(flights) glimpse(flights)## Rows: 336,776 ## Columns: 19 ## $ year 2013, 2013, 2013, 2013, 2013, 2013, 2013, 2013, 2013, 2… ## $ month 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1… ## $ day 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1… ## $ dep_time 517, 533, 542, 544, 554, 554, 555, 557, 557, 558, 558, … ## $ sched_dep_time 515, 529, 540, 545, 600, 558, 600, 600, 600, 600, 600, … ## $ dep_delay 2, 4, 2, -1, -6, -4, -5, -3, -3, -2, -2, -2, -2, -2, -1… ## $ arr_time 830, 850, 923, 1004, 812, 740, 913, 709, 838, 753, 849,… ## $ sched_arr_time 819, 830, 850, 1022, 837, 728, 854, 723, 846, 745, 851,… ## $ arr_delay 11, 20, 33, -18, -25, 12, 19, -14, -8, 8, -2, -3, 7, -1… ## $ carrier "UA", "UA", "AA", "B6", "DL", "UA", "B6", "EV", "B6", "… ## $ flight 1545, 1714, 1141, 725, 461, 1696, 507, 5708, 79, 301, 4… ## $ tailnum "N14228", "N24211", "N619AA", "N804JB", "N668DN", "N394… ## $ origin "EWR", "LGA", "JFK", "JFK", "LGA", "EWR", "EWR", "LGA",… ## $ dest "IAH", "IAH", "MIA", "BQN", "ATL", "ORD", "FLL", "IAD",… ## $ air_time 227, 227, 160, 183, 116, 150, 158, 53, 140, 138, 149, 1… ## $ distance 1400, 1416, 1089, 1576, 762, 719, 1065, 229, 944, 733, … ## $ hour 5, 5, 5, 5, 6, 5, 6, 6, 6, 6, 6, 6, 6, 6, 6, 5, 6, 6, 6… ## $ minute 15, 29, 40, 45, 0, 58, 0, 0, 0, 0, 0, 0, 0, 0, 0, 59, 0… ## $ time_hour 2013-01-01 05:00:00, 2013-01-01 05:00:00, 2013-01-01 0… flights$origin as.factor(flights$origin) flights$dest as.factor(flights$dest) summary(flights%>%select(origin, dest, air_time))## origin dest air_time ## EWR:120835 ORD : 17283 Min. : 20.0 ## JFK:111279 ATL : 17215 1st Qu.: 82.0 ## LGA:104662 LAX : 16174 Median :129.0 ## BOS : 15508 Mean :150.7 ## MCO : 14082 3rd Qu.:192.0 ## CLT : 14064 Max. :695.0 ## (Other):242450 NA's :9430We’ll create a dataset containing only flights from Newark and Laguardia to O’Hare, and only the variables we’re interested in.
Flights_NY_CHI flights %>% filter(origin %in% c("EWR", "LGA") & dest =="ORD") %>% select(origin, dest, air_time) summary(Flights_NY_CHI)## origin dest air_time ## EWR:6100 ORD :14957 Min. : 87.0 ## JFK: 0 ABQ : 0 1st Qu.:108.0 ## LGA:8857 ACK : 0 Median :113.0 ## ALB : 0 Mean :114.8 ## ANC : 0 3rd Qu.:120.0 ## ATL : 0 Max. :198.0 ## (Other): 0 NA's :622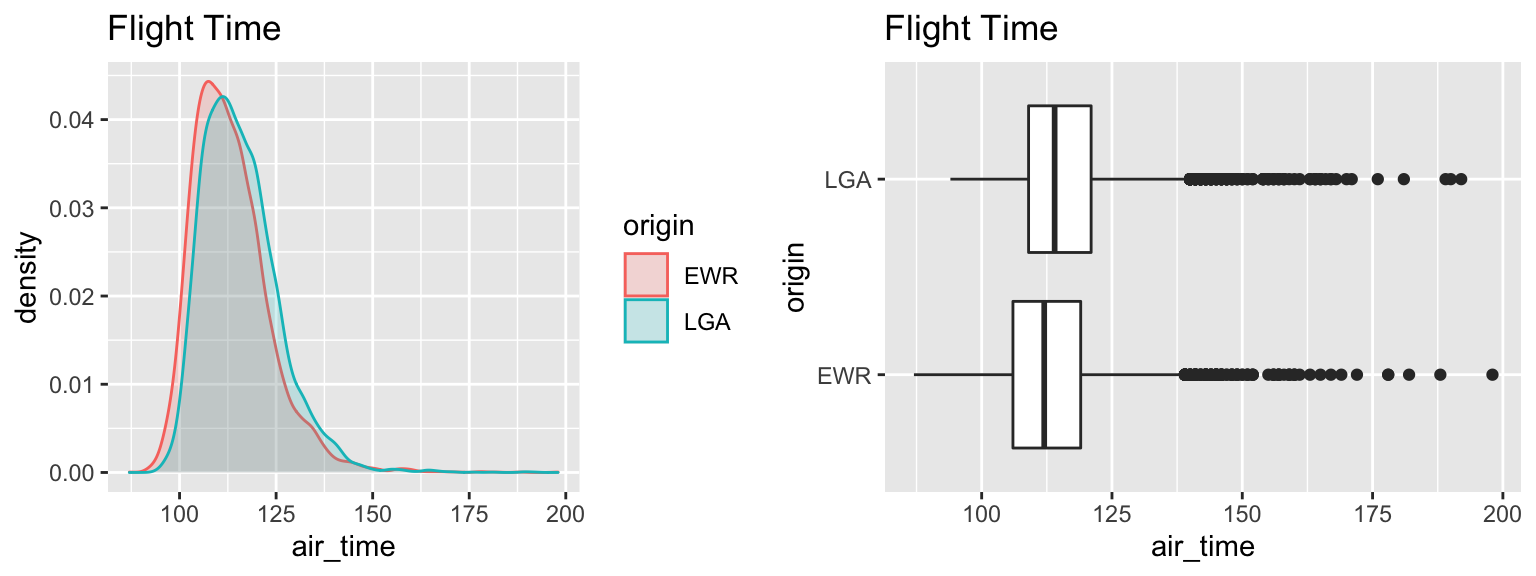
| origin | Mean_Airtime | SD | n |
|---|---|---|---|
| EWR | 113.2603 | 9.987122 | 5828 |
| LGA | 115.7998 | 9.865270 | 8507 |
M_Flights lm(data=Flights_NY_CHI, air_time~origin) summary(M_Flights)## ## Call: ## lm(formula = air_time ~ origin, data = Flights_NY_CHI) ## ## Residuals: ## Min 1Q Median 3Q Max ## -26.26 -7.26 -1.26 5.20 84.74 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 113.2603 0.1299 872.06 confint(M_Flights)## 2.5 % 97.5 % ## (Intercept) 113.00572 113.514871 ## originLGA 2.20905 2.869984Would you base your decision of which airport to fly out of on this information?
Although we have a low p-value, indicating a discernable difference, the size of this difference (2-3 minutes in airtime) is very small. A travelor would most likely have other, more important considerations when deciding which airport to fly from.
The low p-value is due to the very large sample size, rather than the size of the difference.
Note: there is also some question about whether it is appropriate to use a hypothesis test or confidence interval here at all. We have data on all flights in 2013, so one could argue that we have the entire population already. Perhaps, we could view this as a sample and generalize to flights in other years, though conditions change, so it is not clear that these flights from 2013 would be representative of flights in other years.
We consider data on the relationship between a pregnant mother’s smoking and the birthweight of the baby. Data come from a sample of 80 babies born in North Carolina in 2004. Thirty of the mothers were smokers, and fifty were nonsmokers.

| habit | Mean_Weight | SD | n |
|---|---|---|---|
| nonsmoker | 7.039200 | 1.709388 | 50 |
| smoker | 6.616333 | 1.106418 | 30 |
M_Birthwt lm(data=NCBirths, weight~habit) summary(M_Birthwt)## ## Call: ## lm(formula = weight ~ habit, data = NCBirths) ## ## Residuals: ## Min 1Q Median 3Q Max ## -6.0392 -0.6763 0.2372 0.8280 2.4437 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 7.0392 0.2140 32.89 confint(M_Birthwt)## 2.5 % 97.5 % ## (Intercept) 6.613070 7.4653303 ## habitsmoker -1.118735 0.2730012Many studies have shown that a mother’s smoking puts a baby at risk of low birthweight. Do our results contradict this research?
Should we conclude that smoking has no inpact on birthweights? (i.e. accept the null hypothesis?)
Notice that we observed a difference of about 0.4 lbs. in mean birthweight, which is a considerable difference.
The large p-value is mosty due to the relatively small sample size. Even though we observed a mean difference of 0.4 lbs, the sample is to small to allow us to say conclusively that smoking is associated with lower birthweights.
This is very different from concluding that smoking does not impact birthweight.
This is an example of why we should never “accept the null hypothesis” or say that our data “support the null hypothesis.”
In fact, this sample of 80 babies is part of a larger dataset, consisting of 1,000 babies born in NC in 2004. When we consider the full dataset, notice that the difference between the groups is similar, but the p-value is much smaller, providing stronger evidence of a relationship between a mother’s smoking and lower birthweight.
M_Birthwt_Full lm(data=ncbirths, weight~habit) summary(M_Birthwt_Full)## ## Call: ## lm(formula = weight ~ habit, data = ncbirths) ## ## Residuals: ## Min 1Q Median 3Q Max ## -6.1443 -0.7043 0.1657 0.9157 4.6057 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 7.14427 0.05086 140.472 p-values are only (a small) part of a statistical analysis.